java语言基础补码



个人理解：

        书本中给的教科书式的公式是：补码=~原码+1。

        如果我们从为了方便负数的的算术运算层面来理解，那么这个公式应该是：补码+原码=溢出数（例如4位字长的二进制数：1111+0001 = 10000（2^4））。

        为什么这么说呢？我们拿最简单的负数运算来举例，我们来看 -1+1=0这个运算，用4位的二进制数来表示，负数位置由于我们不知道应该如何表示，那就暂时这么表示：-1+0001=0000，我们很自然的就可以想到，这里面的0000是可以通过位的溢出来实现，因此0000可以用10000（2^4）来表示，那么这个-1就应该是1111，这样才能保证-1+1=0（这个0其实相当于10000（2^4），只不过高位1溢出丢弃了）。

        补码+原码=溢出数，此公式经过转换，可以变型为：补码=(溢出数-1-原码)+1，而(溢出数-1-原码)=~原码（原码的取反），举例来说明一下：10000-1=1111，1111-0001=1110，1110就是0001的取反，进而推导出1110=10000-1-0001，因此也就推导出来开头所说的公式：补码=~原码+1。

        我理解补码这个概念就是这么定义出来的，这样就可以通过高位溢出的方式来实现负数的加法运算了，因为溢出位可以直接丢弃，并不会影响运算结果，加法和减法可以使用相同的电路来实现，所以非常的方便。

        由于当代计算机是利用“电”特性来实现的，因此0和1很自然的就成为计算机中数据的表示。而我们日常生活中的算术运算，对于计算机来说，0和1的位运算（逻辑运算）更容易实现，因此计算机是用位运算（逻辑运算）来实现的算术运算（比如加法器的实现）。

PS：用4位二进制数举例子是因为8位太长了，道理都是相同的，位数太长没啥必要，还挺费眼睛的。

        为了方便各位做实验来验证，下面给出“打印二进制数”的算法（就是从高位到低位，从左到右依次的把各个位打印出来，简单易懂，而且简洁；比对2求余数或者右移1位并且和1进行与运算的实现方式要好。另外我英语不好，为了方便自己可以用眼睛快速定位到需要的信息，所以类名就使用中文来命名了。）：

​​​​​​​

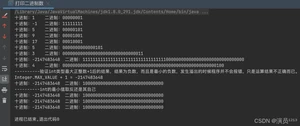
关于“计算机中信息的表示形式”的理解：

        计算机中是用0和1这种数字串来表示信息的，其实和数学中的二进制还是有一些却别的，数学中的二进制111表示的是7，而计算机中为了运算方便，111表示的是-1（假设3bit的字长）。

        我们举个简单并且具体的例子来说明我要表达的意思（为了方便，假设字长就是3bit）：

• 假设我们数学中有8个数字要表示，分别是：的0、1、2、3、-1、-2、-3、-4；
• 而在计算机中：

1. 数字0就用000表示、数字1就用001表示、数字2就用010表示、数字3就用011表示，这都很符合我们的思维。
2. 那么数字-1应该如何表示呢？根据上面我们对补码的理解，为了方便-1+1=0（其实是1000，3bit字长溢出以后就剩下000了）的运算，-1这个数就用111表示，以此类推，-2+2=0，-2这个数就用110表示，-3这个数就用101表示。
3. 3bit字长一共可以表示2^3个数字，也就是8个数字，而前面我们已经使用的数字组合有：000、001、010、011、111、110、101，我们只剩下100这个数字组合还没有使用了，我们列举一下已经发现的规律：111-1=110（表示-2）、110-1=101（表示-3），根据前面的规律101-1=100，相当于-3-1=-4，因此100用来表示-4，由于100是1开头，表示负数也非常合理。
4. 我们再总结一下上面计算机java语言基础补码中数字串表示的信息和数学中数字的对应关系：000、001、010、011、111、110、101、100分别对应0、1、2、3、-1、-2、-3、-4。
5. 有了上面的对应关系，我们做些运算来验证下，-1+1=0 -> 111+001=1000、-2+2=0  -> 110+010=1000、-3+3=0 -> 101+011=1000，而1000在3bit字长的计算机中发生了溢出，也就是说1000其实就是000，而对于-4我们是没有办法采用上面方式验证的，因为在本例子下，数学中的8个数字中，并不包括4这个数字，所以我们用3来进行运算，-4+3=-1 -> 100+011=111，而111其实就是-1，是不是很神奇。

        总结一下上面的文字想表达的核心思想：

        计算机中的0、1数字串并不能简单的和数学中的二进制数字等价，计算机中的数字串仅仅是表示信息的一种编码，上面我们列举的计算机信息的表示方式，就是采用补码形式来表示数学中的数字。

        所以我们可以理解为：计算机中的0、1组成的数字串就是补码，并不是数学中的数字，我们从“补码”这个名称中就可以看出，其中的“码”字就很明显的表示出，就是一种编码而已，并不是数学意义上的数字，只不过“补码”的运算是符合数学规律的（在不发生越界溢出的情况下），或者说“补码”的产生就是为了方便计算机的数学运算而人为定义出来的一种表示数字的“编码”，所以在理解补码的时候一定要和数学中的数字区分开来，不要混淆，否则很容易懵逼。

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.bianchenghao6.com/h6javajc/18761.html