文章目录
- 一、堆
-
- 1.1 堆常用操作
- 1.2 堆的实现
-
- 1.2.1 堆的存储与表示
- 1.2.2 访问堆顶元素
- 1.2.3 元素入堆
- 1.2.4 堆顶元素出堆
一、堆
「堆 heap」是一种满足特定条件的完全二叉树,主要可分为两种类型,如图所示。
- 「大顶堆 max heap」:任意节点的值>=其子节点的值。
- 「小顶堆 min heap」:任意节点的值<=其子节点的值。
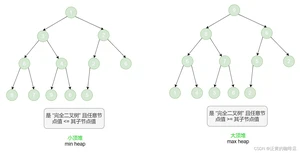
堆作为完全二叉树的一个特例,具有以下特性 - 最底层节点靠左填充,其他层的节点都被填满。
- 我们将二叉树的根节点称为“堆顶”,将底层最靠右的节点称为“堆底”。
- 对于大顶堆(小顶堆),堆顶元素(根节点)的值分别是最大(最小)的。
java基础类型堆
1.1 堆常用操作
需要指出的是,许多编程语言提供的是「优先队列 priority queue」,这是一种抽象数据结构,定义为具有优先级排序的队列。
实际上,堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构。因此,本书对两者不做特别区分,统一称作“堆”。
以下是根据文中内容整理的关于堆数据结构的相关方法的表格:
在实际应用中,我们可以直接使用编程语言提供的堆类(或优先队列类)。
类似于排序算法中的“从小到大排列”和“从大到小排列”,我们可以通过设置一个 flag 或修改 Comparator 实现“小顶堆”与“大顶堆”之间的转换。代码如下所示:
1.2 堆的实现
下文实现的是大顶堆。若要将其转换为小顶堆,只需将所有大小逻辑判断取逆(例如,将 >= 替换为 <= )。
1.2.1 堆的存储与表示
“二叉树”章节讲过,完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此我们将采用数组来存储堆。
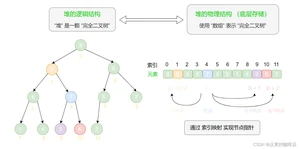
当使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置。节点指针通过索引映射公式来实现。
如图所示,给定索引 i,其左子节点索引为 2i+1 ,右子节点索引为 2i+2,父节点索引为 (i-1)/2(向下整除)。当索引越界时,表示空节点或节点不存在。
1.2.2 访问堆顶元素
堆顶元素即为二叉树的根节点,也就是列表的首个元素
1.2.3 元素入堆
给定元素 val ,我们首先将其添加到堆底。添加之后,由于 val 可能大于堆中其他元素,堆的成立条件可能已被破坏,因此需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为「堆化 heapify」。
考虑从入堆节点开始,从底至顶执行堆化。我们比较插入节点与其父节点的值,如果插入节点更大,则将它们交换。然后继续执行此操作,从底至顶修复堆中的各个节点,直至越过根节点或遇到无须交换的节点时结束。
设节点总数为n,则树的高度为O(log n)。由此可知,堆化操作的循环轮数最多为O(log n),元素入堆操作的时间复杂度为O(log n)。代码如下所示:
1.2.4 堆顶元素出堆
堆顶元素是二叉树的根节点,即列表首元素。如果我们直接从列表中删除首元素,那么二叉树中所有节点的索引都会发生变化,这将使得后续使用堆化进行修复变得困难。为了尽量减少元素索引的变动,我们采用以下操作步骤。
- 交换堆顶元素与堆底元素(交换根节点与最右叶节点)。
- 交换完成后,将堆底从列表中删除(注意,由于已经交换,因此实际上删除的是原来的堆顶元素)。
- 从根节点开始,从顶至底执行堆化。
“从顶至底堆化”的操作方向与“从底至顶堆化”相反,我们将根节点的值与其两个子节点的值进行比较,将最大的子节点与根节点交换。然后循环执行此操作,直到越过叶节点或遇到无须交换的节点时结束。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/h6javajc/2859.html
