什么是数据结构?
对大规模数据进行合理的规划,提高操作效率
什么是时间复杂度?
用来描述算法的运行时间的函数
如何快速判断时间复杂度?
1.直接对问题规模下手。O(n)
2.循环减半 O(logn)
3.k层循环 O(n的k次方)
数组
无序数组查找的时间复杂度为O(logn)
无序数组排序为有序数组的时间复杂度 O(n²)/O(nlogn)
1.将无序数组变为有序数组,用2分查找法O(logn)
2.利用某种算法来决定数据插入的位置 n%arr.length
缺点:覆盖原来的值
数组通过下标获取值 O(1)
创建数组必须确定数组长度,且数组长度不可变
数组的扩容
1.在数组长度不够的时,创建一个新的比原来数组更长的新数组
2.让原数组中的数字依次复制到新数组中
3.让arr指向brr,数据存入
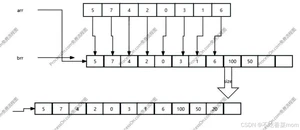
数组的插入
在最后位置插入
1.判断在数组有没有位置,没位置了考虑扩容
用size记录当前数组有效数据的个数,判断满没满就是看size和arr.length是否相等,相等则满了,考虑扩容,不等则可以添加,size指向有效数据后一位
2.在下标是size的位置插入,size++
在指定位置插入
1.判断位置的取值是否合理 [0,size]
2.判断现在数组有没有位置,没位置了考虑扩容用size记录当前数组有效数据的个数,判断满没满就是看size和arr.length是否相等,相等则满了,考虑扩容,不等则可以添加
3.把原来的数组当中想要插入的位置及其之后的数据,按照从后往前的顺序,统一往后移动一位,避免数据被覆盖
4.数据移动完成之后,原来的数据就不怕被覆盖了,在目标位置插入新数据 size++
有序数组插入数据
找位置进行插入
1.判断现在数组有没有位置
用size记录当前数组有效数据的个数,判断满没满就是看size和arr.length是否相等,相等则满了,考虑扩容,不等则可以添加
2.找位置
[数组有效长度为0时]:arr[0]直接插入 size++
[要插入的为最大值时]:value>arr[size-1] arr[size]直接插入size++
[其他情况]:和指定位置插入一样,先找位置,找到第一个比插入数据大的,即目标位置
目标位置极其之后的数据,按照从后往前的顺序,依次向后移动,size++
数组的删除
把数据覆盖掉,有效数据长度减少
指定位置删除
判断删除位置是否合理 [0,size-1]
目标位置之后的数据整体向前覆盖,以从前到后的顺序 size--
时间复杂度:O(n)
指定数据删除
1.找到要删除的数据,从后往前找,找到后记录其所在的位置
2.目标位置之后的数据,按照从前往后的顺序,统一向前覆盖
3.size--,继续向前查找要删除的数据
找:O(n)+删:O(n)
时间复杂度:O(n)
补充:双指针
慢指针:需要更新的下标
快指针:获取新数组所需要的元素
如果fast指针遇到需要删除的元素,直接跳过,fast++。否则将该值赋值给慢指针,fast++,slow++
size=slow
栈
先进后出的特点
限制线性表(数组,链表)中元素的插入和删除
插入和删除在同一端进行
允许插入和删除的一端为变化端,称为栈顶
另外一端称为栈底
插入数据:
定义栈顶,初始值为-1, 栈顶++
出栈:取出数据,栈顶--
判断栈满:每一次入栈都要判断栈是否满,满了之后考虑扩容
设置数组长度为maxsize,则maxsize-1指向数组的最后一个位置
插入之前判断栈顶和maxsize-1是否相等,相等则栈满
判断栈空:每一次出栈前都要判断栈是否为空,栈顶为-1则表示栈空

树
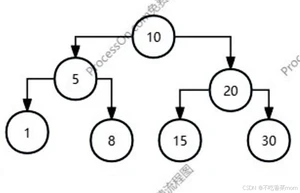
有序二叉树
节点左边的值要小于该节点,右边的值要大于该节点
比如:
平衡二叉树
节点左边的值要小于该节点,右边的值要大于该节点
一个节点,左边子树的高度和右边子树的高度高度差的绝对值不能超过1
如果超过了就会导致二叉树不平衡,此时就要进行旋转
平衡二叉树的四种旋转 LL LRRR RL
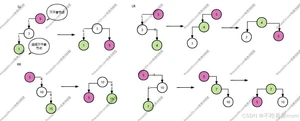
此时查找的时间复杂度为O(logn)
平衡二叉树的缺点:消耗计算机资源较高
由此引出红黑树,即最优二叉树(内存最优)
红黑树
特点
每个节点不是红色就是黑色
根节点永远是黑色
每个叶子节点都是黑色,并且值是null
如果一个节点是红色的,那么它的子节点一定是黑色
从根节点到任意一个叶子节点路径上黑色节点数目相同
♛在红黑树上没有一条路径比其他路径长超过两倍,最多两倍
最短路径:黑+黑+黑
最长路径:黑+红+黑+红+黑+红
哈夫曼树和哈夫曼编码
哈夫曼编码是一个变长编码
路径:从根节点开始到该节点所走过的路线
路径长度:路径上边的条数
边:父子节点之间的连线
节点的权:节点的值
带权路径长度:从根节点到该节点之间的路径长度与该节点的权值的乘积
树的带权路径长度:所有叶子节点的带全路径长度之和
最短带权路径长度WPL就是哈夫曼树
如何构造哈夫曼树?
1.将带构造哈夫曼树的节点(按权值)从小到大进行排序,每个数据都看成一个节点
2.取出根节点权值最小的两个二叉树
3.组成一棵新的二叉树,新的二叉树根节点的权值就是这两个二叉树根节点节点权值之和
4.将这个二叉树以根节点的权值大小再次进行排序
不断的重复上述步骤,直至所有的数据都被处理,就得到了哈夫曼树
如何按照给定的某个英文句子构造哈夫曼树呢?
比如: i like bananas
1.统计各个字符出现的次数
2.按照出现的次数构建哈夫曼树,次数作为权值
3.根据哈夫曼树给各个字符编码向左的路径为0,向右的路径为1
多叉树
一个节点上可以分出多个叉
B树(磁盘最优):一个节点包含多个key值 value值
key:给每一个文件进行标号(主键)
value:页(存储数据的地址)
每个节点都包含key和value,根据key值找value值
二节点-包含一对key-value值,能分出两个叉
三节点-包含两对key-value值,能分出三个叉(三个next域)
四节点-包含三对key-value值,能分出四个叉
五节点-包含四对key-value值,能分出五个叉
♛每个节点中的key值按照从小到大的顺序排列
一个M阶B树(一棵B树由M个参数构建)
1.每个节点里最多有M-1个k值,并且key值以升序排序
2.每个节点最多有M个子节点
根节点有子节点,则至少有两个子节点
B+树(一般用于数据库的底层的数据查找)
特点:1.B+树的非叶子节点仅具有索引作用(只能存key值不能存value值)不包含真正的数据
2.B+树的所有叶子节点构成有序链表
例如构建五阶B+树
内存相同的情况下,B+树能存更多的key值,树的高度降低
B+树的叶子节点都是相连的,对整棵树的遍历只需遍历叶子节点即可,便于区间查找(数据库底层)
排序
选择排序
基本思想:1.默认待排序数组中的第一个数为最小值2.找待排序数组中真正的最小值和待排序数组中的第一个数据进行交换每一轮都可以让一个数据到达正确位置
时间复杂度:O(n²)
java基础复习笔记 数据结构插入排序
1.认为数组中的第一个值已经排好序了
2.定义一个游标从第二个数值开始不断向后进行遍历
3.游标指向的数据插入已经排好序的数组当中
如何进行插入?
定义游标j指向i的前边,让j和j+1进行比较
如果j指向的值更大,则两个数据进行交换,然后j--,继续进行比较(当arr[j]<arr[j+1]或者j<0时,该数据插入成功)
时间复杂度:O(n²)
♛越小的数据在后面移动的次数越多
希尔排序(缩小增量排序)
1.将数组按照数组长度的一半为间隔进行分组,组内进行插入排序
2.将数组按照数据长度的一半的一半为间隔进行分组,然后组内进行插入排序
3.将数组按照数据长度的一半的一半的一半为间隔进行分组
直到间隔为1,整个数组为一组,进行插入排序,整个数组排序完成
时间复杂度:O(nlogn)
快速排序
1.定义待排序数组当中的第一个值作为基准值
2.j游标从后往前移动,找比基准数小的数值,找到后停止
3.i游标从前往后移动,找比基准数大的数值,找到后停止
4.i和j进行交换
5.重复2 3 4直到i和j相遇
6.基准数和相遇位置进行交换,这时候基准数到达正确位置
7.以基准数为起点,分成左右两部分,重复上述所有,直到数据都被拆分开为止
简单描述:定一个数为基准数,然后定义两个游标(i和j)分别从前/从后开始遍历,如果找到一个数比已知基准数小/大,就把这个数放在该基准数的左/右,如果i指向的数比基准数要大,则二者交换,i++,(j指向的值比基准数小,则二者交换,j--)
每一轮的时间复杂度为O(n)
时间复杂度:O(nlogn)
基数排序
定义0-9十个桶(二维数组),先排序个位,再排序十位,再排序百位……
时间复杂度:O(kn)
♛k不能省略
堆排序
1.利用完全二叉树构建大顶堆
2.堆顶元素和堆底元素交换,除堆底元素外剩余的元素继续构建大顶堆
3.不断重复2,直到排序完成
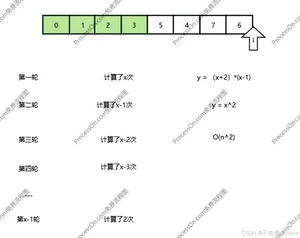
什么是完全二叉树?
数据必须从上到下从左到右的顺序排列的二叉树
比如 5 7 4 2 0 3 1 6 的完全二叉树为
什么是大顶堆?
父节点的值大于或等于其左右节点的值
从后往前检测完全二叉树的节点是否符合大顶堆要求,如果符合,检测前一个节点。如果不符合,对该节点进行维护,让其符合大顶堆
如何检测+维护呢?
1.定义parent游标指向该节点
2.定义parent的左孩子👶🏻child child=2×parent+1判断有没有左孩子,如果没有左孩子,那么该节点符合大顶堆。
3.如果有左孩子,判断有没有右孩子(有孩子一定会有左孩子)
4.如果有右孩子,左右孩子进行比较,让child指向左右孩子中的最大值
5.父子节点进行比较
6.如果父节点的值大,该节点符合大顶堆,继续向前检测
7.如果子节点的值大,那么父子节点进行交换(交换完成后,parent指向child,child指向左右孩子的最大值,继续parent和child进行比较,直到parent的值大或者child为空)
时间复杂度:O(nlogn)
归并排序
先拆分,再合并(时间复杂度:O(n)),在合并的过程中借用临时空间进行排序
拆分:从中间位置拆开,数据分成左右两部分。继续拆分,直到拆分成一个一个的时候停止 O(logn)
时间复杂度:O(nlogn)
链表
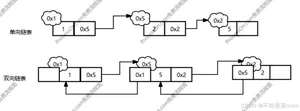
单项链表

双向链表

添加
尾插法

head储存链表头节点的地址
1.判断head是否为空,如果为空,直接插入
2.如果不为空,定义游标遍历整个链表,找到链表当中最后一个节点
(最后一个节点的next域为空NULL)
3.插入i->next=node(node为新节点地址)
头插法

1.判断head是否为空,如果为空的话直接插入
2.如果head不为空,新节点的next域将链表当中第一个节点的地址存下来node->next=head
3.head指向新节点 head=node
链表遍历
定义游标i从前到后遍历,i=head
输出当前节点的值i->value
i=i->next
直到i为空结束,整个遍历完成
输出链表的长度

定义一个变量count,每遍历一个数据,让count+1 最后输出变量的值
查找链表元素
每遍历一个数据,查看当前节点的value域和目标值是否相等,相等则找到了,不能找下一个,直到全部遍历完成
插入
指定位置插入
1.判断插入位置是否合理[0,链表长度]
2.如果在0号位置插入,头插法
3.如果在最后位置插入,尾插法
4.如果在中间位置插入,先找出目标位置的节点i以及目标位置前一个节点pre,i指向的节点成为新节点的下一个节点 node->next=i,新节点成为pre的后一个节点 pre->next=node
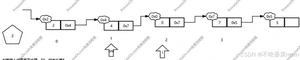
指定位置删除
1.判断删除位置是否合理[0,链表长度-1]
2.删除的位置为0号节点 则 head=head->next
3.删除中间位置的节点 先找出目标位置的节点i以及目标位置前一个节点pre,pre->next=i->next
4.删除尾节点 pre->next=i->next
队列
先进先出
队尾:允许插入的一端(下面用front表示)
队头:允许删除的一端(rear表示)
入队:rear++,插入数据
出队:front++,出队
队满:maxsize-1和rear是否相等,相等则队满
队空:rear和front是否相等,相等则队空
补充:CPU
磁道并不光滑,上面有一个个的小磁颗粒,分为N极和S极
磁头上存在线圈
如果磁头为N极,则磁颗粒为S极,电流方向变化,磁头S极磁颗粒为N极
存入数据:电生磁(电流的方向改变,产生不同的0/1)
读数据:磁生电(线圈不带电,磁颗粒点上有磁感线,磁头划过磁感线产生电流,N/S产生的电流不同,只需要一个感应电流的装置就可以知道是N还是S极,对应由此得来0/1的数据)
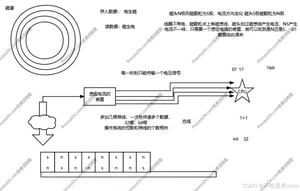
为什么用电压信号呢?
电阻不变(3欧)的情况下-电流公式:电流×电阻=电压
功率公式:电流×电压=功率
假设用电流表示信号量:电流1A->3A
电压:3V->9V,功率:3W->27W
假设用电压表示信号量:电压1V->3V
电流:1/3A->1A,功率:1/3W->3W
🌵功率消耗小,所以选择电压控制
一根导线(即总线)一时刻只能传输一个电压信号,效率很低,因此多增加几根导线,一次性就能传递多个数据
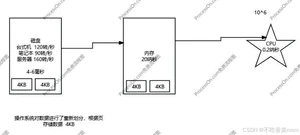
由于磁盘和CPU的速度差距很大(CPU价格很昂贵),由此引入内存
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/h6javajc/19479.html
