java基础编程实验



1 实验目标概述

本次实验通过求解四个问题，训练基本Java编程技能，能够利用Java OO开发基本的功能模块，能够阅读理解已有代码框架并根据功能需求补全代码，能够为所开发的代码编写基本的测试程序并完成测试，初步保证所开发代码的正确性。另一方面，利用Git作为代码配置管理的工具，学会Git的基本使用方法。

l 基本的Java OO编程

l 基于Eclipse IDE进行Java编程

l 基于JUnit的测试

l 基于Git的代码配置管理

2 实验环境配置

1. 安装java18
2. 安装Git
3. 安装Eclipse
4. 设置Eclipse
5. 设置Git和github.mit.edu

https://github.com/ComputerScienceHIT/Lab1-120L021427

3 实验过程

3.1 Magic Squares

要求：给定一个矩阵，并判断其是否是幻方（Magic Square）。矩阵以txt文件形式给出，每一行的数字之间用/t分割。

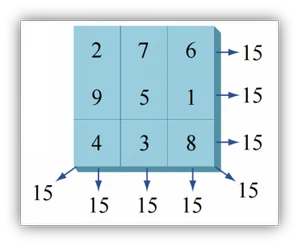
幻方应满足如下条件：

n阶幻方是n*n个数（通常是不同的整数）在一个正方形中的排列，使得所有行、所有列和两条对角线中的n个数之和为相同的常数。

3.1.1 isLegalMagicSquare()

isLegalMagicSquare函数原型：

public static boolean isLegalMagicSquare(String fileName) throws IOException {  }

为实现幻方的判断，我创建了一个名为MagicSquare的类。主要包含以下两个函数public static boolean isLegalMagicSquare以及public static void main

main函数包括读取五个矩阵文件并判断，以及生成一个矩阵并输出到6.txt

文件中。

以下是isLegalMagicSquare函数的主要内容：

读入文件

创建FileReader、BufferReader、StringBuilder对象

逐行将字符串转换为整型矩阵存储

将非空readline的字符串分割，去除头尾空格后转换为数字存储到二维数组中，并且判断数字是否出现过以及行列数是否相等。

计算两条斜线的和并比较

计算每行和每列的和并比较

测试结果：

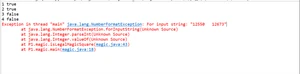
3.1.2 generateMagicSquare()

将要求中给出的generateMagicSquare函数加入到创建的MagicSquare类中并在main函数中测试。

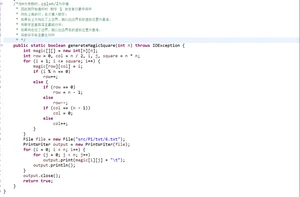
此函数根据输入的参数（奇数n）生成一个n×n的Magic Square，并将矩阵输出到6.txt文件中。

对n为偶数和负数时的异常情况进行分析。

n为偶数:j=n时，row=n-1，执行如下if语句中的row++语句，使得row=n,magic数组下标越界。

流程图：

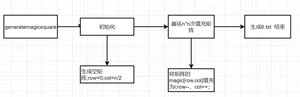
将5.txt文件的错误修改后，进行测试。

测试结果：

当输入n为偶数时，输出Input Wrong:

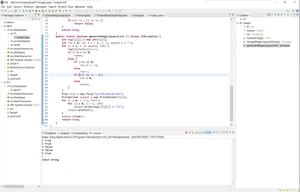
当n为奇数时：

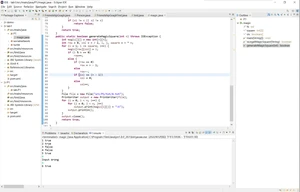
以下为n=5时生成的幻方6.txt。

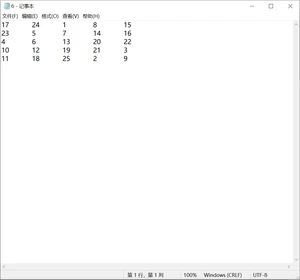
3.2 Turtle Graphics

3.2.1 Problem 1: Clone and import

1. 首先利用给定的URL clone P2代码：

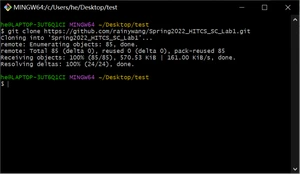　　　　　　 2. 之后将P2代码复制到创建的lab1程序的src目录下

3.2.2 Problem 3: Turtle graphics and drawSquare

该函数需要实现：已知边长，画出边长为指定数值的正方形。参数是turtle和sidelength。

首先将海龟画笔设置为黑色。然后执行4次的前进sidelength长度、转完90度，即可完成一个边长为sidelength的正方形。下图是边长为40的正方形：

代码如下：

3.2.3 Problem 5: Drawing polygons

已知正多边形边数的情况下计算正多边形的内角度。根据几何知识可以推导得公式：

(double)180.0−(double)360.0/sides

使用该公式，实现calculateRegularPolygonAngle

另外在已知正多变型边数和边长的情况下画出一个正多边形。参照画正方形的方法，可以先前进sidelength，再使海龟旋转一个角度，执行“side”次。其中，这个角度是正多边形内角的补角，利用calculateRegularPolygonAngle的功能计算出多边形内角，再用180°减去这个值即可。

边长40的正5边形效果如下：

边长40的正9边形效果如下：

Junit测试代码以及测试结果截图：

3.2.4 Problem 6: Calculating Bearings

实现。calculateBearingToPoint

此函数计算从当前点到目标点所需的参数，并将当前方向作为附加参数。

实现。calculateBearings

请务必在此处使用您的实现。有关如何使用 Java 的接口和实现它的类的信息，请在 Java 库文档中查找 java.util.List。请注意，对于 n 个点的列表，您将返回 n-1 个标题调整;此调整列表可用于将引导到列表中的每个点。

具体实现方法：对于每个target坐标，先计算它相对于当前位置的偏转角θ（代码中的targetBearing），可以通过Math库中的反三角函数实现(弧度制要转化成角度制)；此外，由于反三角函数返回[ −π/2 , π/2 ]中的值，无法区分degree30°和150°需要判断一下target的相对位置。

具体函数如下：

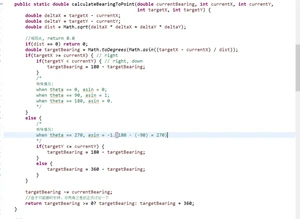
实现calculateBearings: 记录当前位置和朝向，不断调用calculateBearings。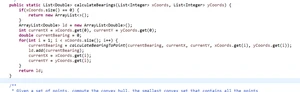

Junit测试：

3.2.5 Problem 7: Convex Hulls

实现：它计算凸壳，即包含一组输入点中所有点的最小凸集。

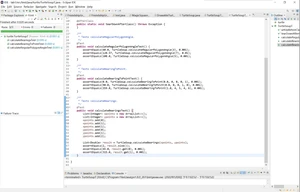
使用礼品包装法解决凸包问题。

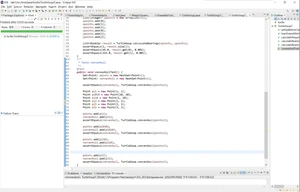
Gift-Wrapping算法描述：对任意凸包上的点，以该点建立一个极角坐标系，该点连结其它所有点的极角中，该点逆时针方向的第一凸包点到该点极角最小。首先找到最左边的点，这个点必然在凸包上，然后计算该点连接点极角最小的，这里计算有技巧，算法中进行toright测试,直到找到到最右端的点，找到P1后，就可以从P1开始，接着顺次找到P2，又以P2为起点……直到结束。代码如下：

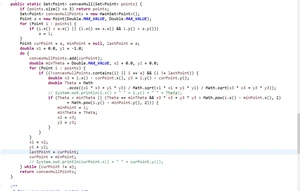
Junit测试：

3.2.6 Problem 8: Personal art

个人艺术：利用turtle实现colorful spiral（彩色螺旋）。

特点：步长step越来越长，并且每一次拐弯变颜色。

密度（density）：数值越小，螺旋线越密集。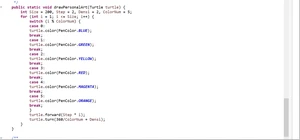

生成图形如下：

如果将Densi改为3：

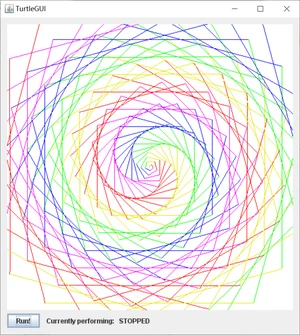
3.2.7 Submitting

3.3 Social Network

该任务要求设计一张社交网络图，基于连接人与人，并且能计算任意两人之间的联系情况。网络图基于两个类，分别是FriendshipGraph类和Person类。

实现FriendshipGraph和Person类，其中FriendshipGraph应该有方法addVertex(加点)，addEdge(加单向边)，getDistance(返回二人最短距离，若不连通返回-1)；Person类有一个String型的name成员。

3.3.1 设计/实现FriendshipGraph类

该类的实际意义是一张社交网络图，包括了代表每个Person的点、代表每两个Person之间联系的边、以及建立点和联系和计算距离的方法。

在存储社交网络时，我使用了邻接表。所有的Node被连在一起，方便查找，并补充了一个head变量用来标记首个Node。

Class FriendshipGragh

FriendshipGragh类要实现的是将一个Person转换为邻接表里的点，所以一个Node有邻接表中点的重要成员变量：下一个Node为next，对应的Person对象person，直接连接的边lastEdge，以及实现邻接表的相关方法。为了能实现方法getDistance，我另外增设了vis和dis两个变量用来记录是否访问过以及与当前起点的最近距离。

Edge

该类是邻接表中的边，每个Edge对象存储了邻接表中的下一条边，以及对应的边的两个Person所对应的Node。

LoadData

该方法将Person对象导入到Node中进行存储，需要的时候可以直接调用。

addNode

该方法将相应的Node加入到Node的链表中（即邻接表图中的纵向链表）。

addNodeEdge

该方法将新的边加入到对应的Node中，更新每个Node后的Edge链表。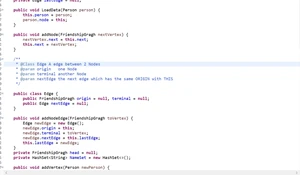

void addVertex()

在社交网络图中增加一个新的节点，参数是要加入的Person类。首先，方法要对Person的名字进行判重：用哈希集合HashSet记录下已加入的所有Person的名字，每当新加入一个Person则进行判断是否在集合中；然后则新建一个Node类，使每一个Person与一个Node对应起来。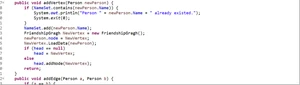

void addEdge()

将两个Person之间进行联系，在邻接表中，用有向边来代表“有社交关系”，由于题目设定是社交默认为双向，则需要在函数中两次调用Node中的addNodeEdge方法加两个方向的边。考虑到可扩展性和可复用性，程序考虑到了“单向社交的情况”，仅需将双向加边中的“B->A”删除即可。

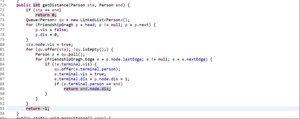
void getDistance()

计算任意两个Person之间的“距离”，若没有任何社交关系则输出“-1”。两个Person之间计算使用BFS，默认边权为1，则在搜索到边时加1即可，搜索到目标点退出；特殊情况根据要求输出0或-1。

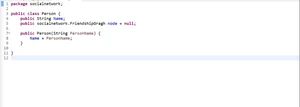
3.3.2 设计/实现Person类

将每一个人对应到一个Person对象，并存储名字的信息。此外，在我的设计中，为了方便起见，我将每个Person对象在FriendshipGraph中对应的Node存储在对应Person的成员变量中。

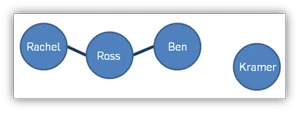
3.3.3 设计/实现客户端代码main()

根据实验要求给出的状态图，进行main函数的构造和测试。

函数：

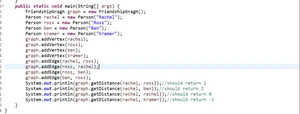
测试结果：

3.3.4 设计/实现测试用例

重复名字错误测试：

当当有重复名字b时，程序是否能终止：

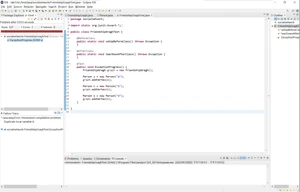
可以看到程序正常运行但出现Error，提示有重复的b。

复杂图测试：

按照如下测试用例进行程序测试。

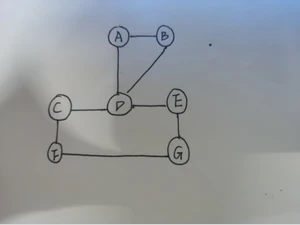
运行Java程序：

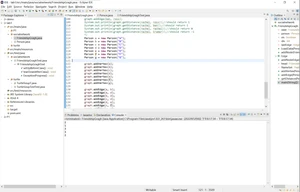
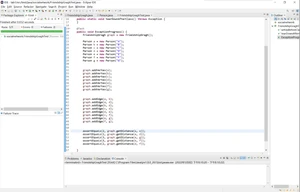
Junit测试：

4 实验进度记录

请使用表格方式记录你的进度情况，以超过半小时的连续编程时间为一行。

5 实验过程中遇到的困难与解决途径

6 实验过程中收获的经验、教训、感想

6.1 实验过程中收获的经验和教训（必答）

Java的编程：掌握了各种对象的使用HashSet等

6.2 针对以下方面的感受（必答）

(1) Java编程语言是否对你的口味？与你熟悉的其他编程语言相比，Java有何优势和不足？

符合。优势：便捷。

(2) 关于Eclipse或IntelliJ IDEA，它们作为IDE的优势和不足；

Eclipse较IDEA的操作较为复杂。

(3) 关于Git和GitHub，是否感受到了它在版本控制方面的价值；

通过指令交互，简洁。

(4) 关于CMU和MIT的作业，你有何感受；

考研编程基本功的同时，还具有一定的创新性。

(5) 关于本实验的工作量、难度、deadline；

工作量较大。

(6) 关于初接触“软件构造”课程；

觉得比较复杂。

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.bianchenghao6.com/h6javajc/19332.html