许多人认为进制转换很复杂,对其中的过程也不太清楚。但是相信阅读完这篇文章后,您会对各种进制转换有一个清晰的认识。
1.十进制:以0-9这九个数字组成。
2.二进制:由0和1两个数字组成。
3.八进制:由0-7数字组成,不存在8和9。
4.十六进制:由0-9和A-F组成。A-F对应的是10-15。
「 一、十进制转二进制 」
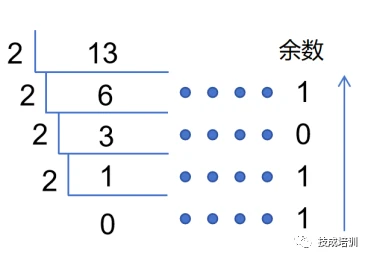
1.十进制转二进制:一直除以2直到商为0,再反向取余数。
例:13(十进制)转1101(二进制)
2.二进制转十进制:最后一位数开始是2^0,然后一直按照指数递增的方式进行加法运算
例:10110(二进制)转22(十进制)

「 二、十进制转八进制 」
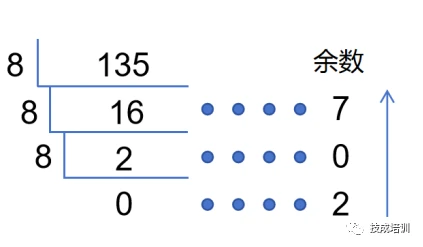
1. 十进制转八进制:一直除以8直到商为0,再反向取余数。
例:135(十进制)转207(八进制)
2. 八进制转十进制:最后一位数开始是8^0,然后一直按照指数递增的方式进行加法运算;
例:634(八进制)转412(十进制)

三、十进制转十六进制 」
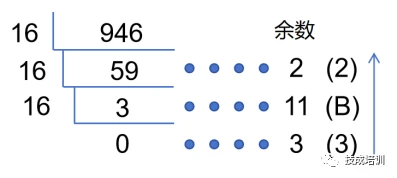
1. 十进制转十六进制:一直除以16直到商为0,再反向取余数。
例:946(十进制)转3B2(十六进制)
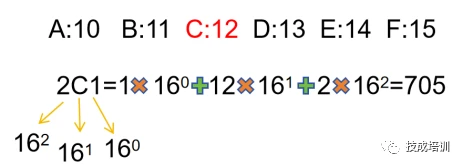
2. 十六进制转十进制:最后一位数开始是16^0,然后一直按照指数递增的方式进行加法运算
例:2C1(十六进制)转705(十进制)
四、二进制转八进制 」
1. 二进制转八进制:最后一位数开始取三合一,不够3位前面补0,参照下图顺序排列取得八进制数。

例:(二进制)转273(八进制)
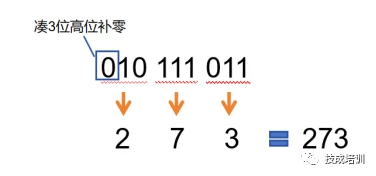
2. 八进制转二进制:操作反过来,取一分三。将1个八进制数分为3个二进制数,参照下图顺序排列取得二进制数。

例:316(八进制)转(二进制)
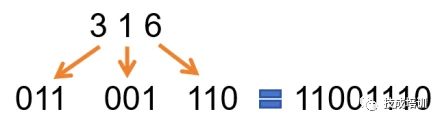
「 五、二进制转十六进制 」
1.二进制转十六进制:最后一位数开始取四合一,不够4位前面补0。再用8421码的方法顺序排列取得十六进制数。
例:(二进制)转4B6(十六进制)
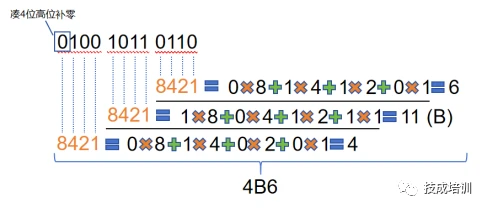
2. 十六进制转二进制:所有数拆分成1位,再用8421码的方法顺序排列取得二进制数。高位为0可省略。
例:38D(十六进制)转(二进制)
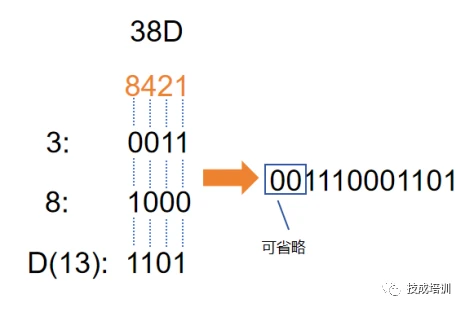
文章来源:技成培训网原创,作者:范腾楷;未经授权禁止转载,违者必究!
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/h6javajc/18582.html
