Hi，大家好，我是编程小6，很荣幸遇见你，我把这些年在开发过程中遇到的问题或想法写出来，今天说一说牛顿迭代法求平方根√3_用牛顿迭代法求平方根,希望能够帮助你!!!。

牛顿迭代法
求出根号a的近似值：首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后x的值就已经相当精确了。 
例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了： 
( 4 + 2/4 ) / 2 = 2.25 
( 2.25 + 2/2.25 ) / 2 = 1.56944.. 
( 1.56944..+ 2/1.56944..) / 2 = 1.42189.. 
( 1.42189..+ 2/1.42189..) / 2 = 1.41423.. 
…. 
 

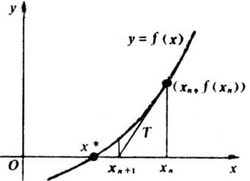
这种算法的原理很简单，我们仅仅是不断用(x,f(x))的切线来逼近方程x^2-a=0的根。根号a实际上就是x^2-a=0的一个正实根，这个函数的导数是2x。也就是说，函数上任一点(x,f(x))处的切线斜率是2x。那么，x-f(x)/(2x)就是一个比x更接近的近似值。代入 f(x)=x^2-a得到x-(x^2-a)/(2x)，也就是(x+a/x)/2。 
 

float my_sqrt(float number) {

    float new_guess;
    float last_guess;
    
    if (number < 0) {

        printf("Cannot compute the square root of a negative number!\n");
        return -1;
    }
    
    new_guess = 1;
    do {

        last_guess = new_guess;
        new_guess = (last_guess + number / last_guess) / 2;
        printf("%.15e\n", new_guess);
    } while (new_guess != last_guess);
    
    return new_guess;
}

今天的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。