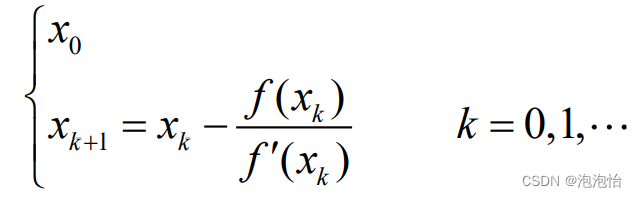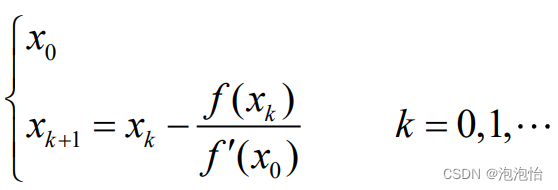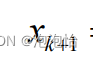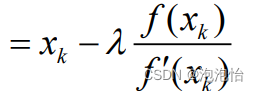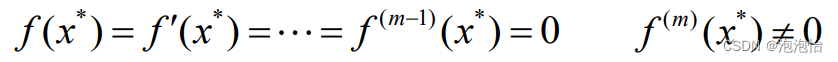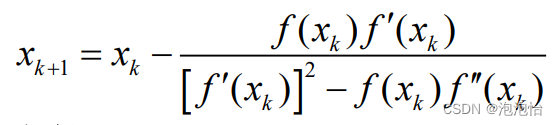非线性方程求根迭代公式的收敛性_牛顿迭代法解方程的N-S流程图
Hi,大家好,我是编程小6,很荣幸遇见你,我把这些年在开发过程中遇到的问题或想法写出来,今天说一说非线性方程求根迭代公式的收敛性_牛顿迭代法解方程的N-S流程图,希望能够帮助你!!!。
一、牛顿法
1.实质:牛顿法实质上是一种线性方法,其基本思想是将非线性方程f(x)=0逐步归结为某种线性方程来解。
2.牛顿法公式:
已知方程f(x)=0有近似解xk,假设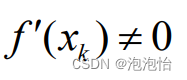
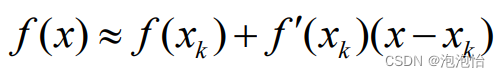
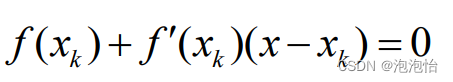
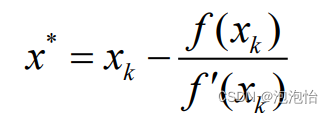
3.牛顿法几何意义:
方程发f(x)=0的根
例题:
牛顿法的优点是收敛快,缺点是计算量大且计算求导困难,并且只有初始近似x0在x*的附近才能保证收敛,若x0不合适可能不收敛。
二、牛顿法改进
1.简化牛顿法迭代公式:
2.几何意义:用斜率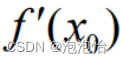

3.牛顿下山法:
(1)基本思想:将牛顿法前后两次迭代结果
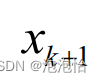
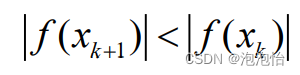
(2)公式:
三、重根情形
设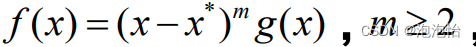
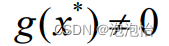

牛顿法: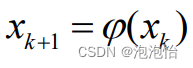
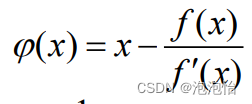
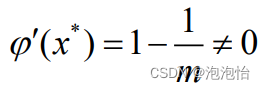
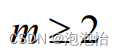
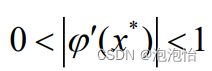
(1)改进一:
取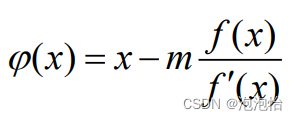
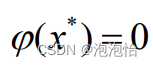
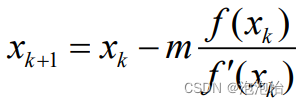
(2)改进二:
若 
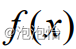
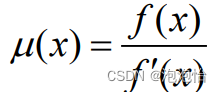

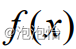
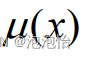
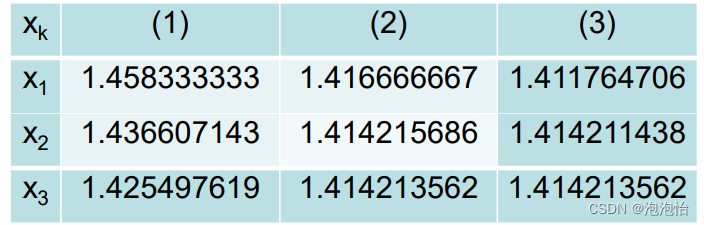
例题:
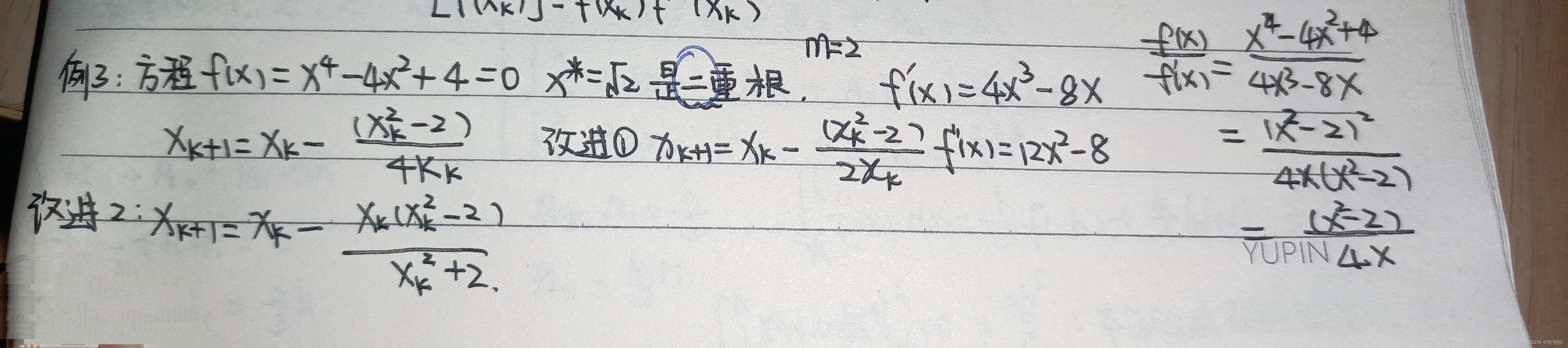
结果:
今天的分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
上一篇
已是最后文章
下一篇
已是最新文章