Hi，大家好，我是编程小6，很荣幸遇见你，我把这些年在开发过程中遇到的问题或想法写出来，今天说一说雅克比迭代法解线性方程组_数值迭代法,希望能够帮助你!!!。

迭代法是一种逐次逼近法，这种方法使用某个固定公式（所谓迭代公式）反复校验根的近似值，使之逐步精确化，直到得到满足精度要求的结果。

迭代法的求根过程分为两步，第一步先提供某个猜测值，即所谓迭代初值，然后再将迭代初值逐步加工成满足精度要求的根。

对于一般的方程 $f(x)=0$, 为使用迭代法，需将它改写成 $x=\phi (x)$$ 的形式，式中 $\phi (x)$ 称迭代函数。

例：求方程 $x^3-x-1=0$ 的唯一正根。先将方程改写成：$x=x^{\frac{1}{3}}$，则迭代函数 $\phi (x)=x^{\frac{1}{3}}$。

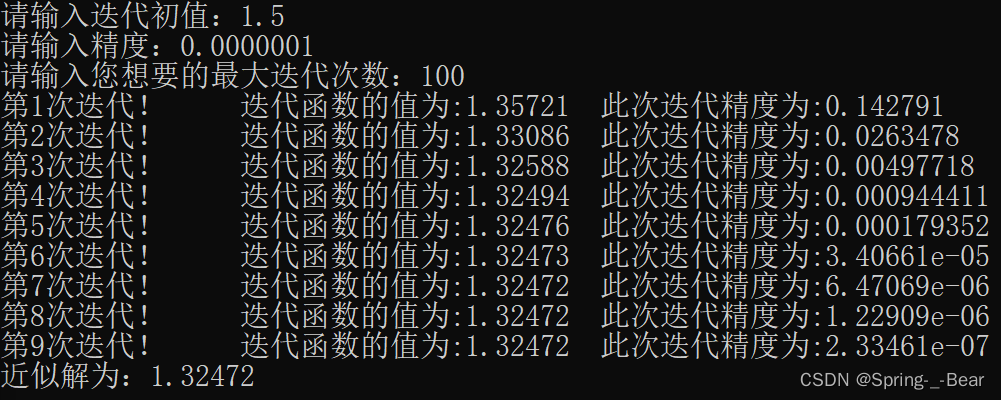
运行示例：

程序源码：

#include <iostream>
#include <cmath>

using namespace std;

/** * f(x) = (x+1)^(1/3) */
double f(double x)
{ 
   
    return pow(x + 1, 1.0 / 3);
}

int main(void)
{ 
   
    double x0;
    cout << "请输入迭代初值：";
    cin >> x0;

    double accrucy;
    cout << "请输入精度：";
    cin >> accrucy;

    int n;
    cout << "请输入您想要的最大迭代次数：";
    cin >> n;

    double x1;
    int count = 1;
    do
    { 
   
        x1 = f(x0);

        if (abs(x0 - x1) < accrucy)
        { 
   
            cout << "近似解为：" << x1 << endl;
            break;
        }

        if (count > n)
        { 
   
            cout << "迭代次数耗尽，迭代结束！未找到符合精度要求的根！！！" << endl;
            break;
        }

        // 继续下一次迭代，直至找到符合精度要求的根或最大迭代次数用完
        cout << "第" << count++ << "次迭代！\t迭代函数的值为:" << x1 << "\t此次迭代精度为:" << abs(x1 - x0) << endl;
        double item = x0;
        x0 = x1;
        x1 = item;
    } while (abs(x0 - x1) >= accrucy);

    return 0;
}

今天的分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。