整数运算
整数的数值表示不但是精确的,而且整数运算永远是精确的,即使是除法也是精确的,因为两个整数相除只能得到结果的整数部分:
求余运算使用:
特别注意:整数的除法对于除数为0时运行时将报错,但编译不会报错。
要特别注意,整数由于存在范围限制,如果计算结果超出了范围,就会产生溢出,而溢出不会出错,却会得到一个奇怪的结果:

要解释上述结果,我们把整数和换成二进制做加法:
由于最高位计算结果为,因此,加法结果变成了一个负数。
要解决上面的问题,可以把换成类型,由于可表示的整型范围更大,所以结果就不会溢出:
还有一种简写的运算符,即,,,,它们的使用方法如下:
Java还提供了运算和运算,它们可以对一个整数进行加1和减1的操作:
注意写在前面和后面计算结果是不同的,表示先加1再引用n,表示先引用n再加1。不建议把运算混入到常规运算中,容易自己把自己搞懵了。
在计算机中,整数总是以二进制的形式表示。例如,类型的整数使用4字节表示的二进制如下:
可以对整数进行移位运算。对整数左移1位将得到整数,左移两位将得到整数:
类似的,对整数28进行右移,结果如下:
如果对一个负数进行右移,最高位的不动,结果仍然是一个负数:
还有一种无符号的右移运算,使用,它的特点是不管符号位,右移后高位总是补,因此,对一个负数进行右移,它会变成正数,原因是最高位的变成了:
对和类型进行移位时,会首先转换为再进行位移。
仔细观察可发现,左移实际上就是不断地×2,右移实际上就是不断地÷2。
位运算是按位进行与、或、非和异或的运算。
与运算的规则是,必须两个数同时为,结果才为:
或运算的规则是,只要任意一个为,结果就为:
非运算的规则是,和互换:
异或运算的规则是,如果两个数不同,结果为,否则为:
对两个整数进行位运算,实际上就是按位对齐,然后依次对每一位进行运算。例如:
上述按位与运算实际上可以看作两个整数表示的IP地址和,通过与运算,可以快速判断一个IP是否在给定的网段内。
在Java的计算表达式中,运算优先级从高到低依次是:
记不住也没关系,只需要加括号就可以保证运算的优先级正确。
也可以将结果强制转型,即将大范围的整数转型为小范围的整数。强制转型使用,例如,将强制转型为:
要注意,超出范围的强制转型会得到错误的结果,原因是转型时,的两个高位字节直接被扔掉,仅保留了低位的两个字节:

因此,强制转型的结果很可能是错的。
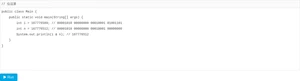
计算前N个自然数的和可以根据公式:
(1+N)×N2frac{(1+N) imes N}22(1+N)×N
请根据公式计算前N个自然数的和:
从 下载练习: (推荐使用IDE练习插件快速下载)
下载练习: (推荐使用IDE练习插件快速下载)
整数运算的结果永远是精确的;
运算结果会自动提升;
可以强制转型,但超出范围的强制转型会得到错误的结果;
应该选择合适范围的整型(或),没有必要为了节省内存而使用和进行整数运算。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/java-jiao-cheng/16448.html
