快速排序作为排序算法中效率最高的一个算法,重要程度可想而知了。
快速排序时一种基于分而治之的排序算法,其中:
1、通过从数组中选择一个中心元素将数组划分成两个子数组,在划分数组的时候,将比中心元素小的元素放在左子数组,将比中心元素大的元素放在右子数组。
2、左子树组和右子数组也使用相同的方法进行划分,这个过程一直持续到每个子数组都包含一个元素为止。
3、最后,将元素组合在一起以形成排序好的数组。
快速排序的特点:第 i 趟排序中会有 i 个元素出现在最终位置上。

现在重新排列数组,将比中心元素小的放在左边,比中心元素大的放在右边。

重新排列数组的方法如下:
1、指针固定在中心元素上,将中心元素与第一个索引开始的元素进行比较。

2、如果该元素大于中心元素,则为该元素设置第二指针。

3、现在将中心元素与其他元素进行比较,如果到达的元素小于中心元素,则将较小的元素和上次找到的较大元素(second pointer 所指向的元素)交换位置。
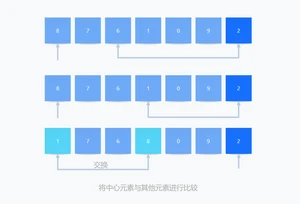
4、同样,重复该过程以将下一个更大的元素设置为第二指针(pointer),并且将其和另一个较小的元素交换位置。
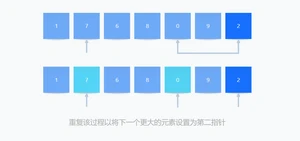
5、该过程一直进行到到达倒数第二个元素为止。
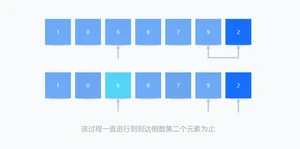
6、最后将中心元素与第二个指针指向的元素交换位置。
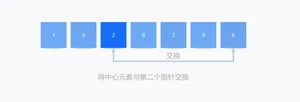
再次分别为左子部分和右子部分选择了中心元素,并且重复步骤2,子数组被分割,直到每个子数组只有一个元素,至此,该数组已经通过快速排序算法升序排好序了。
可以借助以下插图了解快速排序算法的工作原理
- 使用递归对中心元素左侧的元素进行排序
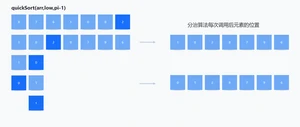
- 使用递归对中心元素右侧的元素进行排序
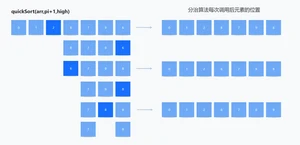
Java 实现快速排序的代码如下:
排序过程的结果如下:
从这个排序结果我们可以知道整个排序过程。
- 最坏的情况复杂度[Big-O] : 当选择的中心元素是最大或最小的元素时发生,这种情况导致中心元素位于已排序数组的最末端,一个子数组始终为空,而另一个子数组包含元素,因此,仅在此子数组上调用quickSort,快速排序算法。
- 最好的情况复杂度[Big-O] : 当中心元素始终是中间元素或靠近中间元素时,会发生这种情况。
- 平均复杂度[Big-O] : 再不出现上述条件时发生。
快速排序的空间复杂度为 O(log n)。
不稳定
快速排序出于性能上的考虑,牺牲了算法的稳定性。虽然可以改变交换规则,使得算法保持稳定性,但却牺牲了性能,对于一个排序算法而言,这是得不偿失的,除非是上下文有稳定性方面的需求,否则,不建议改变交换规则。
在以下情况下使用Quicksort算法
- 编程语言适合递归
- 时间复杂度很重要
- 空间复杂度很重要
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.bianchenghao6.com/java-jiao-cheng/15291.html
